|
Math 2A  Vector Calculus Chapter 11 Test Fall ’07
Name__________________________
Show your work.
Don’t use a calculator. Write
responses on separate paper.
1.
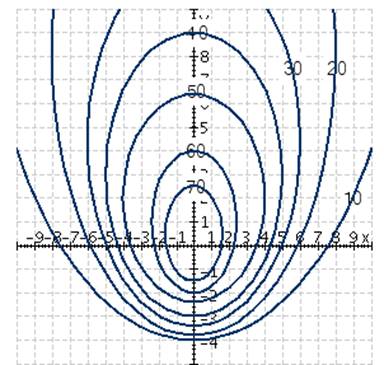
The temperature-humidity index I (or humidex, for short) is the
perceived air temperature when the actual temperature is T and the relative humidity is h, so we can write .
The following table of values of I is
an excerpt from a table compiled by the National Oceanic and Atmospheric
Administration.
|
h
T
|
20
|
30
|
40
|
50
|
60
|
70
|
|
80
|
77
|
78
|
79
|
81
|
82
|
83
|
|
85
|
82
|
84
|
86
|
88
|
90
|
93
|
|
90
|
87
|
90
|
93
|
96
|
100
|
106
|
|
95
|
93
|
96
|
101
|
107
|
114
|
124
|
|
100
|
99
|
104
|
110
|
120
|
132
|
144
|
a.
For what value of h
is ?
b.
Approximate
3.
Find the limit if it exists. If it doesn’t exist, explain why.
a.
b.
4.
Suppose
a.
Find
b.
Find
c.
Find
5.
Find an equation for the tangent plane to the surface
with parametric equations at the point .
6.
Given that ,
x = u v, y
= 2uv, and z = u + v, use the Chain Rule to find and when u
= 4
and v = 5.
7.
The temperature at a point is given by where T
is measured in degrees Centigrade and x,
y, z are in meters.
a.
Find the rate of change of temperature at the point P(0,2,1) in the direction toward the
point (0,5,5). Give your answer in °C/m.
b.
In which direction does the temperature increase
fastest at P? Write your answer as an ordered triple in
the form .
8.
Consider
a.
Find the critical points.
b.
Find all maxima, minima and saddle points in the
first octant.
9.
Find the extreme values of for .
Math 2A Vector Calculus Chapter 11 Test Solutions Fall ’07
1.
The temperature-humidity index I (or humidex, for short) is the perceived air temperature when
the actual temperature is T and the
relative humidity is h, so we can
write .
The following table of values of I
is an excerpt from a table compiled by the National Oceanic and Atmospheric
Administration.
|
h
T
|
20
|
30
|
40
|
50
|
60
|
70
|
|
80
|
77
|
78
|
79
|
81
|
82
|
83
|
|
85
|
82
|
84
|
86
|
88
|
90
|
93
|
|
90
|
87
|
90
|
93
|
96
|
100
|
106
|
|
95
|
93
|
96
|
101
|
107
|
114
|
124
|
|
100
|
99
|
104
|
110
|
120
|
132
|
144
|
a.
For what value of h
is ? SOLN:
b.
Using the formula with the
gradient,
3.
Find the limit if it exists. If it doesn’t exist, explain why.
a.
shows that as we approach the origin along
different lines y = mx, we arrive at a z value that changes…thus the limit does
not exist.
b.
Substitute and . Then (x,y) approaching zero along any path is
equivalent to r shrinking to zero
and we can show the limit exists:
4.
Suppose
a.
Find . SOLN:
b.
=
c.
Find . SOLN: by Foucault’s theorem, this is the
same as above.
5.
Find an equation for the tangent plane to the surface
with parametric equations at the point .
SOLN: Note that the point in question is (u,
v) = (1, 1). Now is a curve along the surface passing through
(0,7,2) when v = 1 and a vector tangent to this curve (and
thus tangent to the surface) is .
Similarly, , which at u = 1 is . Thus a normal to the tangent plane is given
by and an equation for the tangent plane is 7x (y
7) + 7(z
2) = 0.
6.
Given ,
x = u v, y
= 2uv, and z = u + v, find and when u
= 4
and v = 5.
SOLN:
7.
The temperature at a point is given by where T
is measured in degrees Centigrade and x,
y, z are in meters.
a.
Find the rate of change of temperature at the point P(0,2,1) in the direction toward the
point (0,5,5). Give your answer in °C/m.
SOLN: The vector from (0,2,1) to (0,5,5) is whose length is 5. Thus is a unit vector in the direction. The gradient vector is . Thus the directional derivative is
b.
In which direction does the temperature increase
fastest at P? Write your answer as an ordered triple in
the form .
SOLN: As can be seen above, the
gradient vector is in the direction .
8.
Consider
a.
Find the critical points. SOLN:
So we have critical points at (0,0) and .
b.
Find extreme values.
SOLN: From inspection we observe
that along the line y = x, z is zero at (0,0)
and rises to peaks at and and then drops to 0 asymptotically as x and y increase. Similarly, along the line y = x except z is minimized at . To be sure, you could also look at the
second derivative test:
Thus, at (0,0) the discriminant is D = 0, which is inconclusive. But from the above inspection, we can
conclude that (0,0,0) is a saddle point since it’s a local min along y = x and it’s a local max along y
= x .
and
so either way, and looking at the sign of fxx confirms the previous
result.
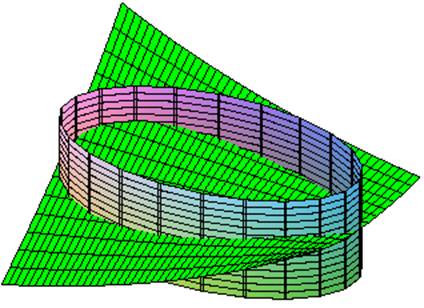
9.
Find the extreme values of for .
|
SOLN: It can be
helpful to make some general observations first. The object function has a saddle point at
(0,0,1) since it is a max along the line y = x and a min along
the line y = x.
Also, the constraint is the interior of an ellipse centered at the
origin with intercepts at (0,1/4) and (1,0).
Here’s a graph of the surface hemmed in by the constraint.
Using the method of Lagrange multipliers, we solve the
system of equations
|
|
This means and, equating components,
Multiplying the first equation through by x
and second through by y we get two
different expressions for xye-xy
so that or, assuming λ≠0, whence the points to look at are and the max occurs where x and y have opposite signs: and the minimum occurs where x and y have the same sign:
|
